在我国,对空之间图的研究起源很早。由于修筑城墙、挖沟等工程需要计算体积,当时的算法在《九章算术》中的“商科篇”和魏晋著名数学家刘徽所著的《九章算术注》中都有介绍。今天,让我们走进历史的长河,看看中国古代数学史上的体积计算。
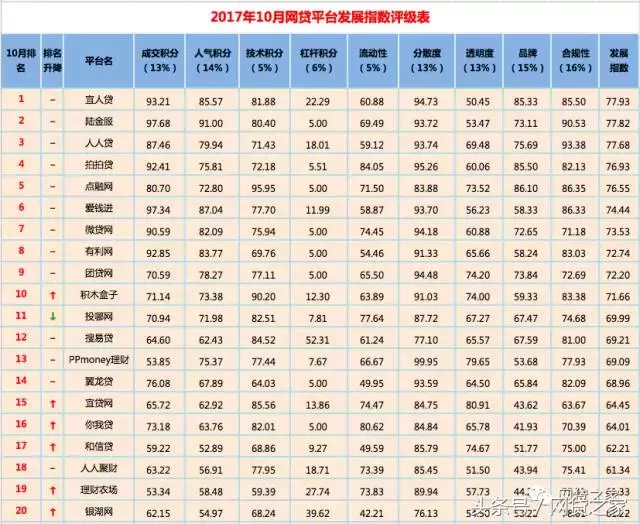
1.堵杨马鳖刘辉在《九章算术笔记》中多次用qiàn、杨马、鳖鳖鳖(nào)等几何来验证和推导立体体积的算法。那么什么是切块、马洋和甲鱼呢?其实我们对这些几何并不陌生。
刘辉首先从几何的角度解释了“割块”(底部为直角三角形的直三棱柱):
魔方的邪恶解决方案有两个障碍;虽然和党复杂,但也是封锁的,所以两个是一个。
这句话的意思是,一个立方体或长方体被一组相对的面的对角线一分为二,得到两个体积相同的块。
刘辉又提到:
推动它的物体,盖子就会叠加在地堑上。
这说明作为实物的切块可能是叠加在切块上的一种设施,或许这就是“切块”这个名字的由来。
什么是沟和马?刘徽赌云:
马的形状是方锥的一角。
意思是公马的形状是四棱锥(正四棱锥)的一个角,他又补充说:
如今,四柱屋的一角是一匹杨。
这是从现实生活情况来解释阳妈所指的实物。
马洋龟是一个面为直角三角形的四面体。刘徽做笔记的时候,重点解释了龟窝的字面意思:
"
臂骨也是手臂的骨头。或半阳马,形似龟肘,因云而得名。
甲鱼刘徽也通过立体分解组合,阐述了切、挡、马洋、甲鱼之间的关系:
"
解决恶的方法有两种,解决恶的问题并不容易。一个是阳马,一个是甲鱼,一个是阳马,第三个是甲鱼。
这意味着一个立方体(立方体或长方体)被斜分解成两个切割块,然后切割块被斜分解得到一个马洋和一只甲鱼。两者的体积比永远是2: 1(难率)。
其实在《九章算术》原著中,《商》给出了“洋马”的体积公式:三个直角边乘积的三分之一。这相当于刘徽后来说的“硬率”(马洋与甲鱼的体积比)。但《九章算术》原文中没有证明。刘徽试图用极限的方法来解释,记载在《九章算术笔记》中。
2刘辉证明杨妈的体积Y与乌龟的体积B之比为2:1并不容易,而且因为切开的体积是半个长方体,所以可以推导出杨妈的体积公式如下
其中a、b和c是长方体三条边的长度。
刘辉认为,命题Y:B=2:1对任何长方体都应该成立,这个比值叫做“硬率”,意思是所有长方体保持相同的比值。刘辉用一个极端的过程给出了他的命题的一般证明。
如图,取公马每条边的中点,将它们连接起来,公马可分为1个小长方体,2个(相同)小沟壑,2个(相同)小公马。
同样,甲鱼也可以分为两个(一模一样的)小甲鱼和两个(一模一样的)小沟壑。
容易获得,公马去掉两匹幼马部分的体积(标为100)是甲鱼去掉两只小甲鱼部分的体积(标为)的两倍,即
com
它们合在一起的体积(刘辉称之为“已知”部分)应占原始采伐体积的1/4。
所以剩余部分(也就是两个小马洋加两个小龟床,刘辉称之为“未知”部分)的体积应该占原切割塞的体积。
如果分别记录每只幼马和龟的体积,则有
其中,和的比例未知。但实际上,我们可以做同样的事情,继续分每一只小马洋和小乌龟,就会有
于是,第一次划分总有“已知”的部分,至于“未知”部分的体积,刘辉指出,随着划分越来越细,会无限趋近于0。刘辉这样描述这个过程:
一半是小的,剩下的没事,到最小的,最小的看不见。你觉得怎么样?
如果我们无限期地继续这个过程,我们将得到极限情况下的“硬率”:Y:B=2:1。
3刘辉的无限思想刘辉的极限法在今天也是非常精彩的。在刘徽的观念中,分割的最终结果是一种“微妙”和“无形”的东西,这可以从他的思想渊源中得到解释。
事实上,刘徽深受墨家思想的影响。墨家曾提出“非半迷人”的命题:
不是半里路就不动了,到最后了。
这就是认为,对于给定长度的木棍,连续做半劈操作,当它拿不下另一半时,就不能用刀砍了。这个时候就会有一个固定的“端”,这里的“端”是指没有大小,测量值为零的东西。
其次,从道家思想来看,刘徽所用的“微”和“无形”两个概念,在刘徽的时代之前是密切相关的。《庄子·秋水》中云:
河伯曰:“凡论天下之人曰:”本质无形...“北海说,”...夫精,小而微;精粗者,望有形;无形,数不可分;不能被包围的人,不能是穷人。"
这里通过“精”的概念把“微”和“不可见”联系起来,体现了道家在精微极小的时候强调“不可见”的极端思想。
刘徽用同样的思维方法提出了著名的“圆的割线”,用正多边形内接的边数不断相乘来逼近圆,从而计算出圆周率:
如果你小心地切,你损失很少。再剪就剪不到了,可以和周长合拍,不损失什么。
刘徽大胆而直接地用无穷过程来处理数学问题,这与我国古代数学注重实在和直觉的传统是一致的。从中国古代哲学的起源来看,刘徽在无限过程的应用上与墨家、道家是一脉相承的。
参考
[1]邹大海,夏,。刘徽对《九章算术》中立体名的认定[J]。自然辩证法通讯,2021,43(04):47-54。
[2]李文林。学一点数学史——谈中学数学教师的数学素养史[J]。数学通报,2011,50(04):1-5。
[3]邹大海。刘辉的无限思想及其解读[J]。自然科学史研究,1995(01):12-21。
转载内容仅代表作者观点
不代表中国科学院物理研究所的立场。
如需转载,请联系原微信官方账号。
来源:大小吴的数学课堂
编辑:*0
本网站声明:网站内容来源于网络。如有侵权,请联系我们,我们会及时处理。
温馨提示:注:内容来源均采集于互联网,不要轻信任何,后果自负,本站不承担任何责任。若本站收录的信息无意侵犯了贵司版权,请给我们来信(j7hr0a@163.com),我们会及时处理和回复。
原文地址"什么叫直三棱柱,直三棱柱图":http://www.guoyinggangguan.com/qkl/149347.html。
微信扫描二维码关注官方微信
▲长按图片识别二维码