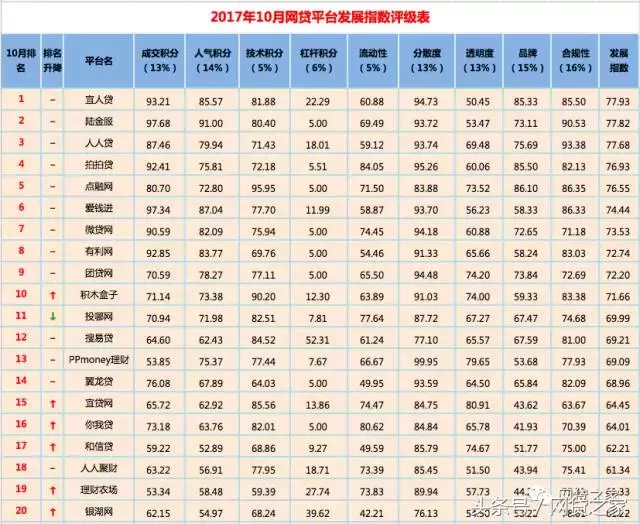
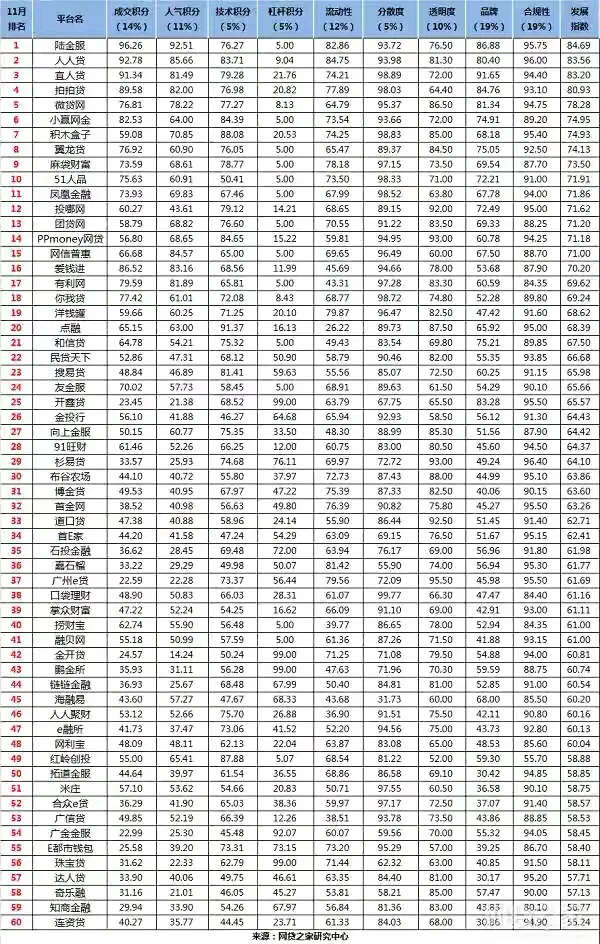
在复杂的密码学领域,零知识证明为一个看似矛盾的任务提供了唯一的解决方案:在不暴露信息本身的情况下证明某个信息的知识。这种加密方法涉及两方:证明者和验证者。证明者的目的是证明他们拥有一些信息(我们称之为X),而不透露任何关于X本身的数据。验证者从通信中了解到的只是一个简单的事实,即证明者拥有这方面的知识。最重要的是,验证者没有得到关于x的额外信息。
比如小零和小十在玩密室逃脱的时候,小零告诉小十他已经破解了一个“宝箱”的密码。但小零不想直接分享现成的“答案”,也不想当着小十的面打开宝箱。那么你怎么向小石证明他真的解谜了,知道宝箱的密码?
于是他让小石在一张只有他自己知道的纸上写下一串,同时签上自己的名字,把纸塞进百宝箱的缝隙里。
然后小玲打开百宝箱,拿出小石放进去的纸,给小石看,小石核对串和签名无误。这证明小玲确实知道宝箱的密码,这张纸也确实是从宝箱里拿出来的。
解密过程小施并不知情,小施证明自己破解了宝箱密码。
零知识证明
在密码学中,零知识证明(ZKP)或零知识协议是一种使证明者能够使验证者相信或证明陈述或断言的真实性而不暴露信息本身或任何其他信息的方法。
零知识证明是由麻省理工学院教授沙菲·戈德瓦瑟、希尔维奥·米卡利和* *查尔斯·罗科夫在论文《交互式证明系统的知识复杂性》中首次提出的。这种算法的概念为现代密码学奠定了一定的基础。
零知识证明有两个额外的属性:简单性和零知识。简单性允许验证者接受大计算的正确性,而不必自己计算语句或语句。零知识确保没有关于输入的数据被泄露。
零知识证明对于保证许多加密协议的私密性和安全性非常重要。他们是防止潜在信息泄露的保障,是密码界的隐形防弹衣。这些知识的应用可以扩展到不同的领域,包括区块链技术和安全认证系统,其中敏感数据的保护是最重要的。
广泛的应用
区块链和加密技术:像Zcash这样的区块链技术使用零知识证明来保护交易隐私。一个人可以证明他们有足够的Cypto货币进行交易,而不需要透露他们资金的确切数额。这确保了交易的隐私和完整性。认证与认证:零知识证明也可以用来确认身份,不会泄露不必要的信息。例如,一个人可以在不提供确切出生日期的情况下证明自己超过18岁,或者在不共享密码等敏感数据的情况下证明自己的身份。这最大限度地降低了身份盗窃或未经授权访问的风险。
安全多方计算(PC):零知识证明可以促进多方之间的复杂交互,在这种情况下,每一方都可以证明他们遵循了约定的协议,而不会暴露他们输入的具体内容。这在很多方面都非常有效,比如保护隐私的数据挖掘,安全的投票系统等等。网络安全:零知识证明可以提供改进的安全协议,比如安全密码策略。它可以在不让服务器知道或记录实际密码的情况下,验证用户提出的密码是否符合某些安全标准。因为密码不会存储在任何地方,所以可以防止潜在的违规行为。共享数据的同时保护隐私:零知识证明可以在不泄露数据本身的情况下证明某些数据满足特定要求,这在医疗或金融领域尤为重要。这些地区对数据隐私有严格的规定,但以安全和保护隐私的方式分享信息可能会带来巨大的好处,例如促进医疗保健的发展。零知识证明在区块链释放了新的技术可能性。这可以在各种层2中看到,例如多边形的ZKSync和zkEVM。然而,这只是由零知识证明创建的区块链的子集。
如何表达一个证明
在这一节和本文的其余部分,我们将重点关注为基于PLONK的证明系统构建的证明。
PLONK是一个零知识证明系统,它的全称是:
“基于拉格朗日基数的全局非交互知识证明安排”,即“基于拉格朗日基数的全局非交互知识证明安排”。
本质上,PLONK是一个通用和可更新的加密证明系统,它允许在区块链系统和其他分布式网络中进行有效的验证和扩展。PLONK背后的想法是建立一个通用的和可更新的证明系统。在零知识证明系统的上下文中,“通用”意味着它可以用于任何类型的计算;“可更新”意味着加密的参考字符串(用于生成和验证证书的一段数据)可以随着时间的推移安全地更新。
PLONK因其高效和简单而备受关注,因此成为需要安全和私密交易系统的项目和公司的热门选择。与其他系统相比,它使用的每个门(计算的基本单位,下面我们将统称为“门”)的约束更少,这使得计算速度更快,可扩展性更强。Vitalik Buterin发表了对PLONK更全面的描述。[* *链接到浏览器查看https://vitalik.ca/general/2019/09/22/plonk.html原著]
证书
在证明一个说法之前,我们先用电路来表达。电路将被计算的值与另外两种类型的数据一起编码:
1.操作:如输入数据的乘法和加法计算。2.操作执行的顺序。
为了对这些数据进行编码,PLONKish电路将被表示为一组向量和约束。约束是向量中的单元必须遵守的关系,其中约束的类型有:门约束和* *约束,分别表示电路中的操作和操作顺序。
对于不同的门和电路架构,有许多方法来表示电路。
将语句表示为一个回路
假设我们有两个门:一个乘法门和一个加法门。乘法门被表示为长度为3的向量|a|b|c|。如果选择这个门,它将约束C等于a * b,同样,加法门表示为长度为3的向量,如果选择加法门,C等于A+B,利用这些门,我们来表示两个向量(A,b)和(C,d)之间的点积。为此,我们需要完成以下计算:1 .用乘法门计算a * b2用乘法门计算c * d3用加法门计算ab+cd,可以用向量表示。
注意,第一和第二乘法门的输出是加法门的输入值。在我们的电路中,该数据独立于门的约束进行编码。这叫* *约束。那么为什么电路约束很重要呢?如果没有约束,那么恶意验证者可以在电路中输入他们喜欢的任何值。例如,验证者可以将ab+cd替换为aba*b B,与智能合约类似,约束在使用前必须经过证明系统的验证。
证明自己的陈述
现在我们可以用电路来表达语句,那么证明者如何说服验证者证明是有效的呢?对于PLONK系统,证明者必须使验证者相信门约束和* *约束已经实现。对于* *约束,这是通过检查排列和组合来实现的。
替换检查首先由Bayer-Groth提出,然后由Gabizon、Williamson和Ciobotaru在PLONK论文中进一步发展。为了证明门的约束,需要计算一个商多项式。
直观上,置换检查表明,如果* *约束项被置换,电路仍然是相同的。替换检查
如果B的所有第I个位置都有σ(i)个位置等于A,我们说一个向量A和一个向量B通过替换σ是相关的。我们表示为σ (a) = b .给定两个向量a=(a,b,& # 8230;,c),b =(a & # 8217;,b & # 8217,…,c & # 8217)$,和排列σ,我们要确定σ (a) = B .这可以通过以下方法来实现:
将向量表示为& # 8217;=((a,1),(b,2),& # 8230;,(c,n))和b & # 8217=((a & # 8217;,σ(1),(b & # 8217,σ(2)),…,(c & # 8217,σ(n))).这是对关于置换σ的向量进行编码。
将向量重写为多项式向量:a & # 8221=((a+1X),(b+2X),& # 8230;、(c+nX))和b & # 8221=((a & # 8217;+σ(1)X),(b & # 8217+σ(2)X),& # 8230;,(c & # 8217+σ(n)X))
查一& # 8221;还有b & # 8221多组是否等价可以通过随机选择gamma来完成,从而显示$(a+1X+γ)(b+2X+γ)& # 8230;。(c+nX+γ)=(a & # 8217;+σ(1)X)+γ)(b & # 8217;+σ(2)X+γ)& # 8230;。(c & # 8217+σ(n)X+γ)$ .
通过随机选择一个β,我们可以用Schwartz-Zippel引理来检验这些多项式是否等价。如果它们作为多项式是等价的,那么集合a & # 8221还有b & # 8221作为多套,是等价的。如果它们不是等价多项式,那么a & # 8221还有b & # 8221它不是一个等价的多集。
写在最后
虽然零知识证明是一门复杂的学科,但它的应用率在不断提高。本文直观地解释了零知识证明的工作原理。未来,CertiK团队将讨论零知识证明的应用,以及团队如何针对新的用例优化其电路。
温馨提示:注:内容来源均采集于互联网,不要轻信任何,后果自负,本站不承担任何责任。若本站收录的信息无意侵犯了贵司版权,请给我们来信(j7hr0a@163.com),我们会及时处理和回复。
原文地址"区块链应用中如何匿名却又保持交易有效 一文带你了解零知识证明":http://www.guoyinggangguan.com/qkl/145077.html。
微信扫描二维码关注官方微信
▲长按图片识别二维码